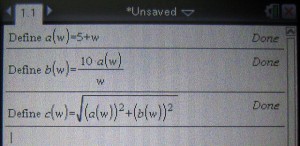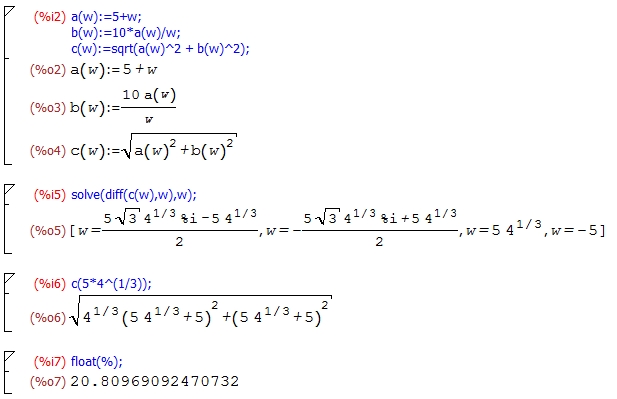今日は日曜日。作業の合間に、関数電卓で少し遊んでみました。
遊ぶといっても、数学の問題集から適当な問題を選んで、電卓で解くとどうなるのかって言うものです。
TI-nspireCX CAS
(比較のためSharp EL-5160J(右)と並べてある)
(画面に映り込みがあってすみません（汗)
今日遊んだ電卓は、Texas Instruments社の 「TI-nspire CX CAS」です。
この電卓は、昨年アメリカで入手したもので、今ではお気に入りの一品です。
現在、日本でも入手可能(Naoco Inc.)ですが、当時アメリカで発見したときは、「何だこの電卓？やけにカッコいいぞ！とりあえずGETだ！」と、勢いで買ってしまいましたｗｗ。
この電卓、使っている方はお分かりになると思いますが、関数電卓というより「ポケコン」という感じです。
また、CAS(Computer Algebra System: 数式処理システム)が搭載されていて、文字、記号を使った代数計算が行えます。
詳しい使い方は、前出のNaoco Inc.社がホームページを充実させてくれているのでそちらをご覧下さいｗｗ。
TIの電卓といえば、教育用に用いられることを強く想定しており、このTI-nspireシリーズも利用の基本概念がとても面白いものです。
教育用電卓として良く出来ているなぁという点は、計算過程を「ドキュメント」や「グラフ」、「表計算」といったノートとして保存し、それらをまとめてをバインダー形式で扱うことが出来ることです。
また、PCを持っている学生は「TI-nspire CAS Student Software」というTI-nspire CASと同機能をもつエミュレータソフトを利用することが出来ます。で、その内容を実機に移して利用することも出来ます。
TI-nspire CXを使った授業を想定してみると、先生方はこのバインダー形式で作られた問題を生徒に配布し、生徒はこの電卓を家でも通学途中のバスの中ででも宿題として勉強することが出来るという事でしょうか。
例えば、TI-89 Titaniumのクイックガイドに載っていた例題を解いてみましょう。
（TI-Nspire CAS Student Softwareを利用せず、画面の写真を掲載します）
■Maximum Length of Pole in Hallway
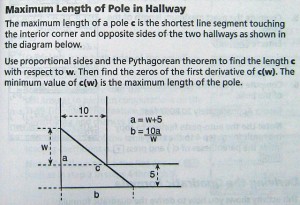
Maximum Length of Pole in Hallway
この問題は、右図のように示された壁にはさまれた通路のコーナー（角）を棒を持って曲がるとき、曲がることの出来る最長の棒の長さはいくつでしょうか？というものです（コーナーは直角です）。
勉強としては、右図のb辺に平行で、角acの頂点からwの場所にある補助線（図では点線部分）は自分で考えなければならないところだと思いますが、ここではTI-nspire CX CASを使っての例題として最初から示されているものとします。
図を見ていただければ直ぐにお分かりになると思いますが、wが変化するときのこの問題は辺cの最長の長さを求めればよいという事です。
棒を一番長くしてコーナーを曲がるとするならば、実感をお持ちの方も居るでしょうが、棒はコーナーの内側の壁にピタリとくっつけて、両端は外側の壁に押し付けるように動かせば良いですね。
では、右図から辺cが棒の長さを示しているので、辺a,bを使って表すと、三平方の定理より、
となります。
ここで、角acの頂点から辺bと平行に辺aに補助線を延ばした交点までの距離をwとすると、辺aと辺bの長さはそれぞれ以下のようになります（図参照）。
これを辺cに代入すると、以下の式が得られます。
ここまでくれば後は簡単ですね。上式のcが最大となるwの値を求めればよいことになります。
ただし、wはw>0でなければなりません。また、cは辺の長さなので正の実数でなければなりません。
このことを踏まえて、wがいくつのときcが最大値をとるのか求めてみましょう。
辺cの値がどのように変化するかわかりませんが、最大値（最小値）を持つということは、極値があるに違いない（考え方は浅はかですが・・・ｗｗ）と考えてみます。
さて、極値はどうやって求めるのでしょうか？簡単ですね。上式のc(w)をwで1回微分して0となるwを求めればよいという事になります。
せっかくなので、ここから先はTI-nspire CX CASに解いてもらうことにしますｗｗ。
■例題をTI-nspire CX CASに解いてもらう
（撮影時の画面の反射を防ぐため、反射防止シートを着けましたw。少々暗く見難いかも知れません・・・）
１．まず、ホーム画面から「New Document」を選択します。
New Documentの選択
２．「New Document」を選択すると、どの種類のページを作成しますか？というメニューが表示されます。
今回は計算を行うので、「Add Calculator」を選択します。
ページ選択画面
３．下図は、「Add Calculator」を選択した後に出てくるページです。
最初は何も書かれていません（当然ですが・・・ｗ）。
作ったばかりのノート（Calcurator)
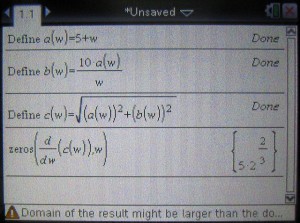
４．まず、a(w)を定義します。式を定義するには、Define関数を使うのですが、この関数は「menu」ボタンを押して出てくるメニューの中から選びます（menuボタン>1:Actions>1:Define）。
Define関数の選択
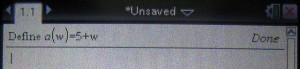
５．Define関数を用いて、a(w)を定義します。
関数a(w)を定義する
６．同様に、b(w)およびc(w)を定義します。
関数b(w)およびc(w)の定義
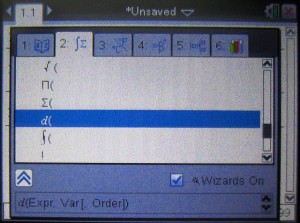
７．関数a(w)、b(w)およびc(w)の定義が終了したら、zeros関数およびdx()（微分）により、c(w)の極値を求めます。
zeros関数は、menuボタン>3:Algebra>4:Zerosから選択し、d()は、ライブラリボタンを押して選択します（dに関してはもっと良い手があるかもしれません）。
微分dをライブラリから選ぶ
８．で、enterボタンを押すと、目的のc(w)関数の極値が求まります。
関数c(w)の極値を求める
９．c(w)の極値が１つ求まりました。
結果は、
（本当は、虚数解も含めて４つになりますが、設定から実数解１つが表示されました）
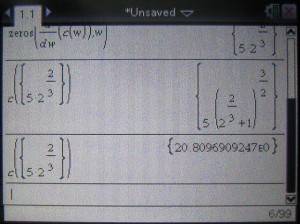
この解では少々見難いので、実数表示にします。
ctrlボタンを押しながら、enterキーを押すと実数の近似解を求めることが出来ます。
この結果、棒の最長は、20.81くらいでしょうかｗｗ。
c(w)の極値におけるwの値（実数解）
このように、文字変数を利用した問題もTI-nspireを用いると簡単に求めることが出来ます。
■例題をMaximaで解いてみた
Maximaはフリーの数式処理アプリケーションで、ご存知の方も多いと思います。
最初にそれぞれの辺の長さをa(w)、b(w)およびc(w)と定義して、solve関数でc(w)を微分したものを解いています。
Maximaによる例題の解法
解として虚数解と実数解が求まりますが、w>0の実数解という事で、
