去る１１月１４日、国会の党首討論で民主党の野田佳彦首相は「今週末１６日に解散してもいい」と条件付ではあるものの、自民党の安倍晋三総裁に提案しました。
野田首相
（毎日jpの写真から）
このことは、街中で号外が出るほどのニュースになり、この記事を書いている現時点では、１２月１６日の衆議院総選挙に向けて各党の選挙活動が活発化しています。
選挙になると各マスコミはこぞって「政党支持率」という「指標」を大々的に我々に提示してくれますが、この「政党支持率」はマスコミ各社によって大小の差があり、どれを信頼していいのか迷ってしまいますよね。
政党支持率とは一体何なのでしょう？何か隠された意味や信頼し得る数字なのでしょうか？
非常に気になります！
そこで、開発日和・・・はこの「政党支持率」について少々調べてみました。
例によって、Wikipedia大先生を見てみると、
「支持率（しじりつ）とは、国の大統領、首相（日本では内閣）、または政党などに対して、国民全体のうちどのくらいが支持しているかを数値化したものである。逆に、支持しない人の割合のことは「不支持率」（ふしじりつ）という。支持率は、百分率（パーセント）で表されることが多い。次の式によって算出される。
アンケートで「支持する」と答えた人の人数 ÷ アンケート調査を行った全体の人数 × 100(%)
この支持率の数値が高いほど、その人や政党の信頼度が高いといえる。日本においては、内閣総理大臣の支持率は主にマスメディア会社によって調査され、その結果はテレビや新聞など発表される。」
とあります。
今回は、アンケートに答えた人（サンプルと呼びます）の偏りやアンケートを実施したマスコミの報道姿勢などを吟味せず、数学的に考えたいと思います。
ネットを調べると、情報って直ぐに調べられるのですね。凄い世の中になりました。
今回は、NHKが発表しているデータを例として使わせていただくことにしました。NHKのデータを使うことに特に意味はありません。思いつきです(無作為！！ｗｗｗ）。
政党支持率
（NHK放送文化研究所 政治意識月例調査より）
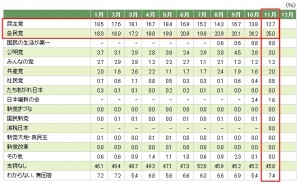
上の表は、NHK放送文化研究所 政治意識月例調査のWebサイトから転載したものです（今回の記事のために、赤線などを引いています）。
この政党支持率を考えるときに必要なのが、「調査対象」ですよね。一体何人の人から、また、どんな人を対象に、どのような方法で調査したのか・・・、などなど。これも気になります。
一般的に得られたデータの「調査対象」は必ず表示されているはずです。これが無ければ、信頼できないデータになってしまいますものね。
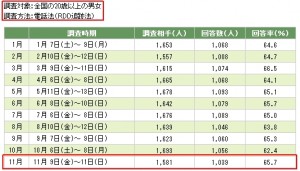
NHK放送文化研究所のWebサイトでも、ちゃんと表示されていました。それが以下の表です。
政党支持率調査対象
（NHK放送文化研究所 政治意識月例調査より）
この２つの表をどのように解釈すればよいか、今回気になるところ-その１-を考えてみます。
【調査対象】
このようなアンケート調査を見るにあたって先ず気にしなければならないのは、「調査対象が本当に民意を反映した支持率になっているのか？」という点です。
つまり、十分な人数の人が答えてくれているのか、アンケートに答えてくれた方に偏りは無いのか？という事です。
国会議員選出などの国民選挙の場合、調査対象は「有権者全員」が最も理想的ですが、時間・コスト的にそれは出来ません。そこで、こう言う場合は「無作為標本抽出（Random Sampling）」という手法がとられます。
無作為標本抽出は、推測統計学という分野で実験的にも理論的にも証明されており、全体のごく一部を調べることにより、大きな母集団の正確な情報がつかめることになっています。
今回提示したデータを見てみましょう。
調査対象は、
調査対象：全国の20歳以上の男女
調査方法：電話法（RDD追跡法）
とあります。
全国２０歳以上の男女における調査ということは、有権者を対象とし、性別は問うて無いので正しい調査対象のように見えます。
また、調査方法は「電話法（RDD追跡法）」とあります。電話法とはどういったものなのでしょうか？
マスコミなどが世論調査などで利用する電話法とは、「無作為ダイヤル法（Random Digit Dial）」と「追跡法」と呼ばれる２つの「多段階サンプリング手法」と考えられます。
つまり、「無作為ダイヤル法」は、国内で使用されている電話番号全てから地域的、人口分布的に偏りが無いように均等な確率で抽出する方法であり、「追跡法」は無作為ダイヤル法で抽出された調査対象に「調査協力依頼」を経て調査実施を行うものです（２段階あるので、多段階サンプリング法といえます）。
これより具体的には、NHK放送文化研究所が行っている調査方法は、「無作為ダイヤル法」で調査対象となった電話番号に調査員が電話をし、その世帯における有権者の有無を確認、その中から無作為に調査対象者を決定していると考えられます。
さらに、そのとき決まった調査対象者が不在の場合には、調査期間中に「再度連絡をするので調査に協力して欲しい」と依頼しておき、その後何度か電話して（追跡）回答を行ってもらいます。
これがNHK放送文化研究所が行っている「電話法（RDD追跡法）」です。
本当に正しく「電話法（RDD追跡法）」を行っているなら、何となくサンプリング方法は正しいように見えますねｗｗ。
【標本数（サンプリング数）】
次に気になるのは、標本数（調査対象の人数）です。
政党支持率調査対象の表より、１１月は、
・調査相手：１５８１人
・回答数 ：１０３９人
・回答率 ：６５．７％
となっています。
果たしてこの人数で、国民全体の政党支持率を反映できるのでしょうか？というのが気になります！
まず、全有権者数（母集団の人数）が有限か無限かを考えると、有限と考えたほうがよい。
総務省のWebサイトを見ると、２０１０年に行われた「第22回参議院議員通常選挙結果」の資料から、母集団の人数は「104,029,135人」となっています。1億４百万人かぁ・・・（とだけ思っておくｗｗｗ）。
これを母集団の人数としておきましょう。
そして、この母集団お人数から一体何人をサンプリングすれば、全体の傾向をよりよく反映していることになるのでしょうか。
1億4百万人を調査できたら最高なのですが、先にも書いたとおり、時間・コスト面でそれは出来ません！
標本調査において、母集団から標本の大きさを決める手法というものがあるのですね。
それは、以下の式で示されています
ここで、
とします。
まず、最大誤差（要求制度）
次に、母集団の比率
ある程度数字を決めたので、上式に従って「必要な標本数」を求めたいと思います。
あっと、
各数字を上式に当てはめると、
となり、
つまり、
統計学的な標本数は、
となります。
となり、
つまり、
統計学的な標本数は、
となります。
上記の計算で、最大誤差を４％、３％および２％として計算してみました。
最大誤差４％ 
最大誤差３％ 
最大誤差２％ 
そっか、この結果から、NHK放送文化研究所の行った政党支持率の電話法による調査は、調査対象が１５８１人で回答数が１０３９人だったので、信頼区間が９９％として誤差３～４％程度で十分有意に信頼できる結果なのかもしれませんね（つまり、有権者全体の意見を反映しているといえるってこと？？）。
納得です！
次は、政党支持率自体の数学的解釈を検討してみたいと思います。
しばらくお待ちくださいねｗｗｗ。
